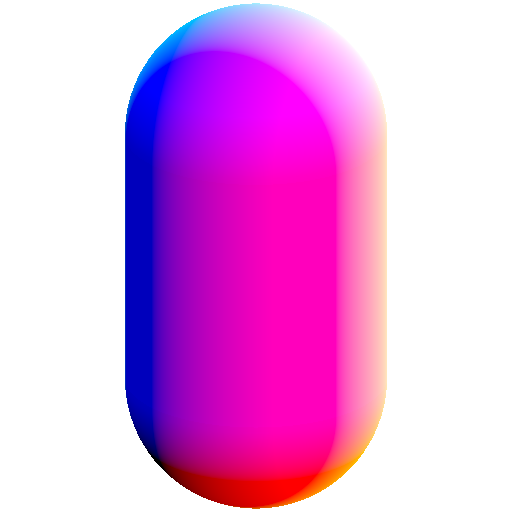
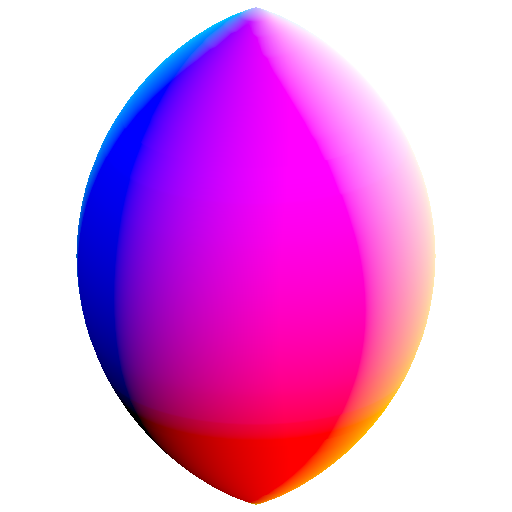

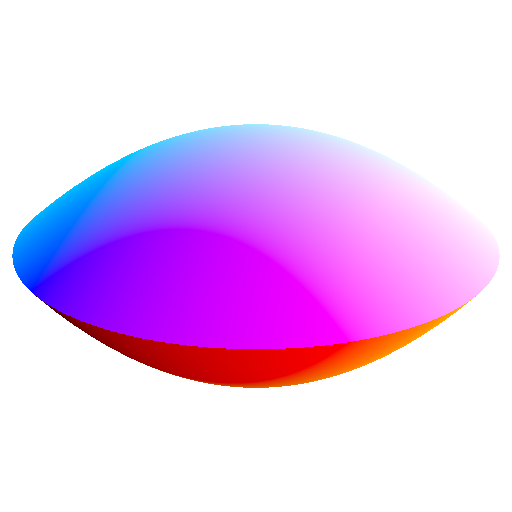
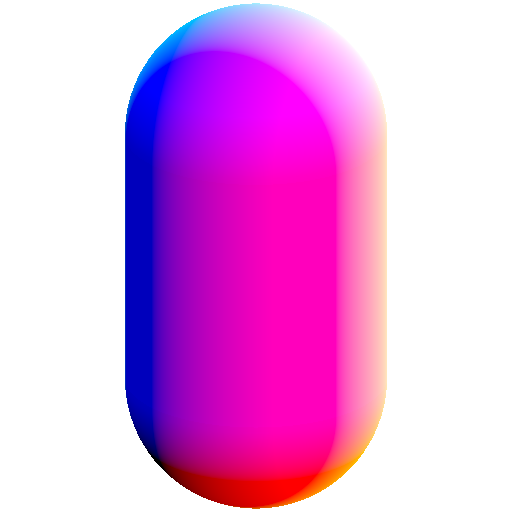

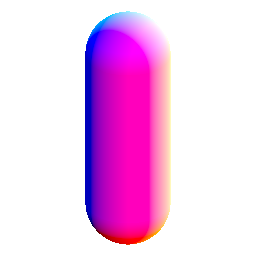

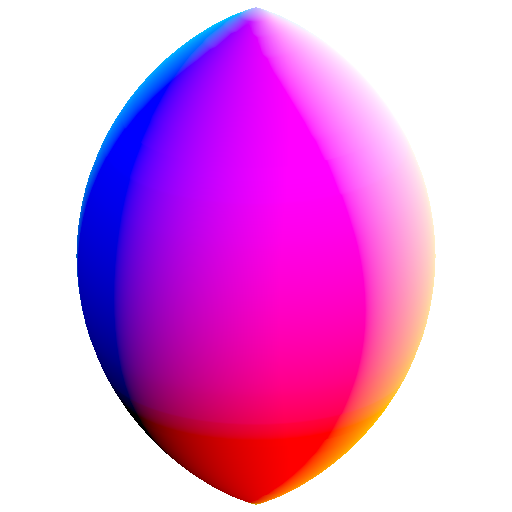


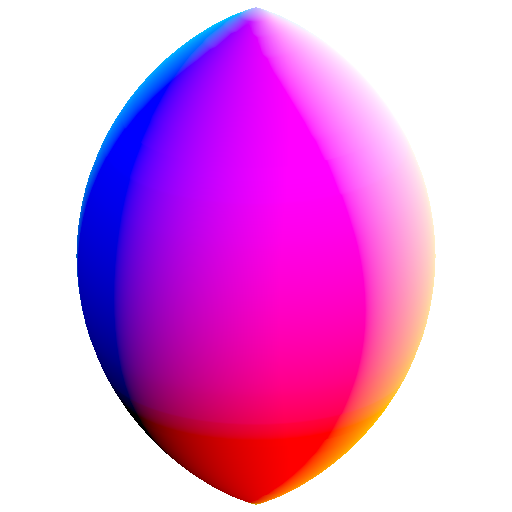



shapes!
im going to add explanations and equations for all this later don't worry
also yes no matter what i do the descriptions like to be to the left of the images instead of underneath them, css is hard
| Image + Name | Description | Symmetry | Dual |
|---|---|---|---|
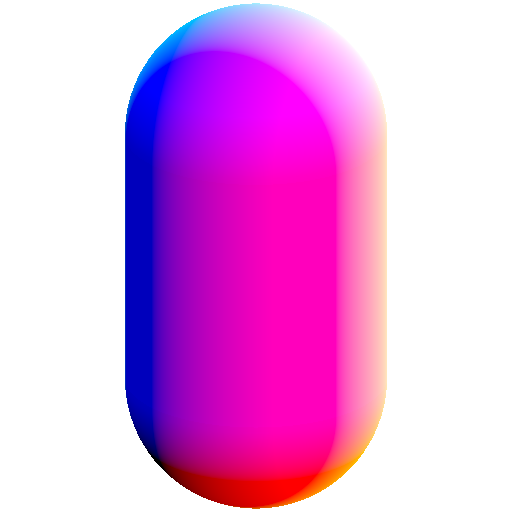 |
|
|
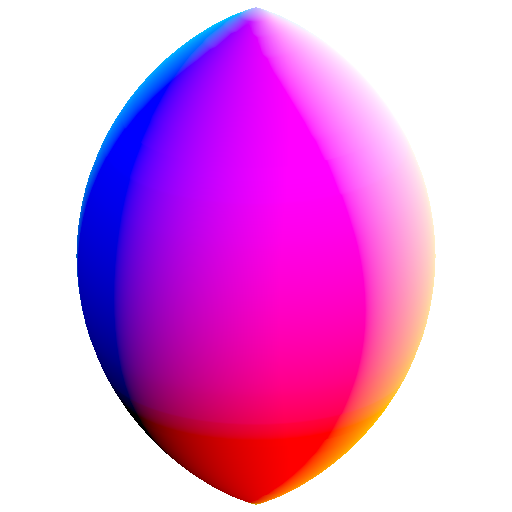 |
 |
|
|
 |
 |
|
|
 |
 |
|
|
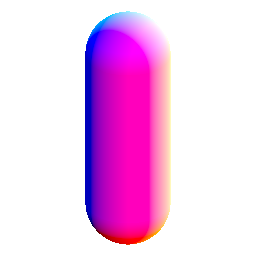 |
 |
|
|
 |
 |
|
|
 |
 |
|
|
 |
 |
|
|
 |
for a capsule with radius 1 and cylinder height 2a, a parametric 2D equation is
( 1, a (2t - 1)) for 0 ≤ t < 1
( cos((t - 1) π), a + sin((t - 1) π)) for 1 ≤ t < 2
( -1, -a (2 (t - 2) - 1)) for 2 ≤ t < 3
(-cos((t - 3) π), -a - sin((t - 3) π)) for 3 ≤ t ≤ 4
for a != 1, its dual biconic has a parametric 2D equation
( 2t - 1, (a - sqrt((2t - 1)² (a² - 1) + 1)) / (a² - 1)) for 0 ≤ t < 1
(-(2(t-1) - 1), -(a - sqrt((2t - 3)² (a² - 1) + 1)) / (a² - 1)) for 1 ≤ t ≤ 2
for a = 1, its dual biconic has a parametric 2D equation
( 2t - 1, 1 / 2 - (2t - 1)² / 2) for 0 ≤ t < 1
(-(2(t-1) - 1), -(1 / 2 - (2t - 1)² / 2)) for 1 ≤ t ≤ 2
torii are surfaces of revolution made from circles whose centers are offset from the center of reciprocation against the axis that the shape isn't being revolved around
their duals are then a surface of revolution of a conic that has a/its focus at the center of reciprocation
| Image + Name | Description | Symmetry | Dual |
|---|---|---|---|
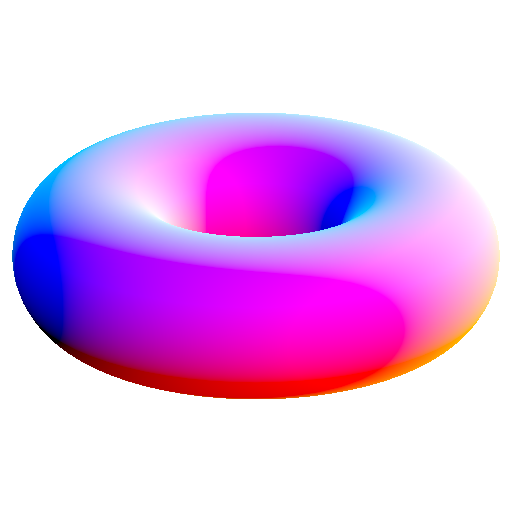 |
|
|
 |
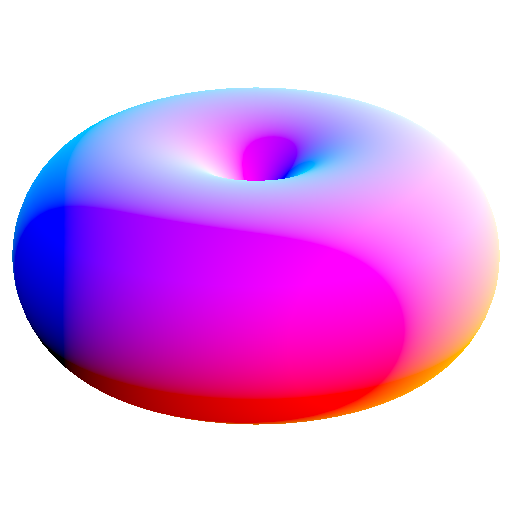 |
|
|
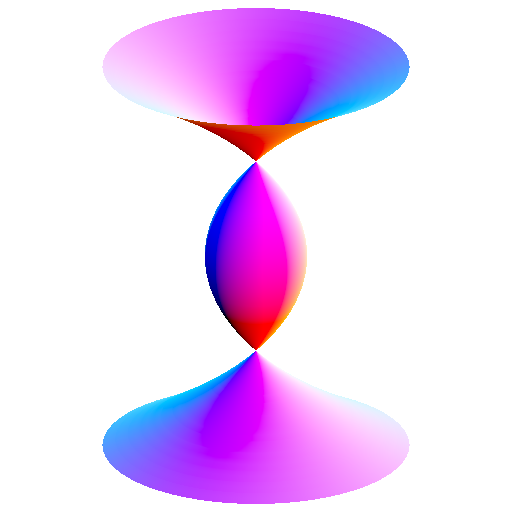 |
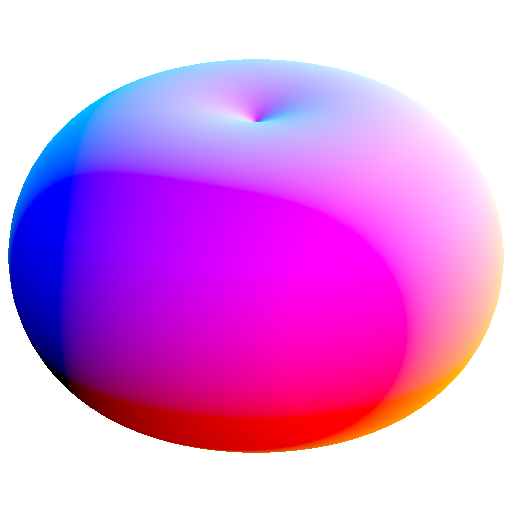 |
|
|
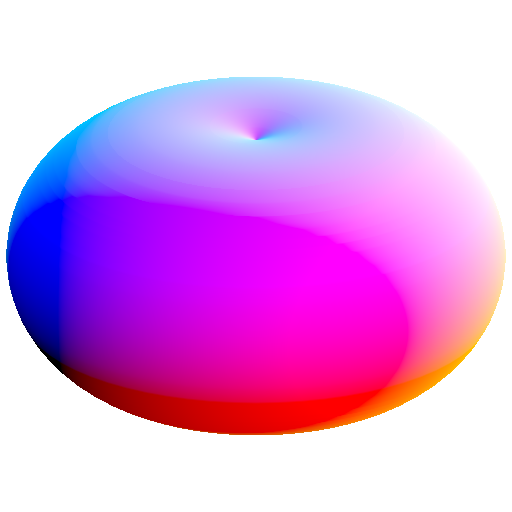 |
 |
|
|
 |
 |
|
|
 |
| Image + Name | Description | Symmetry | Dual |
|---|---|---|---|
 |
|
|
 |
 |
|
|
 |
 |
|
|
 |
 |
|
|
 |
 |
|
|
 |
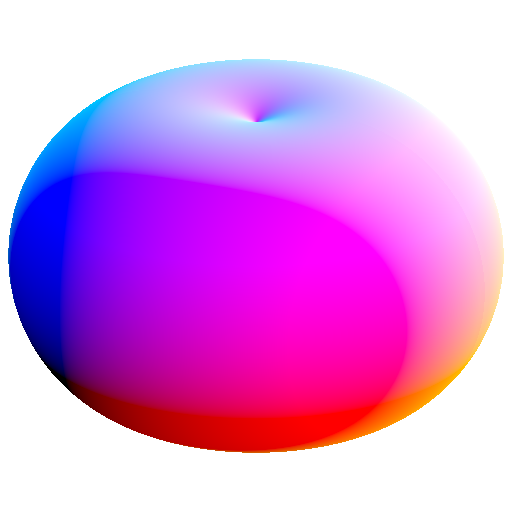
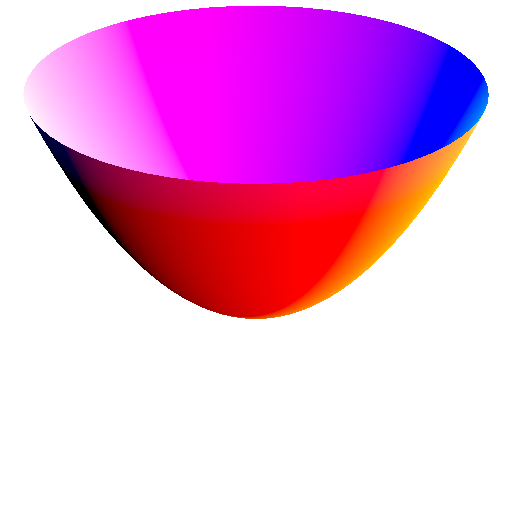
these are spheres whose center is shifted away form the center of reciprocation
because of symmetry, this can be thought of as the surfaces of revolution of a circle whose center is shifted away from the center of reciprocation along the axis of revolution
this produces duals that are a surface of revolution of a conic that has a/its focus at the center of reciprocation
| Image + Name | Description | Symmetry | Dual |
|---|---|---|---|
 |
|
|
 |
 |
|
|
 |
 |
|
|
 |
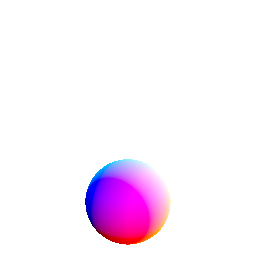 |
|
|
 |
| Image + Name | Description | Symmetry | Dual |
|---|---|---|---|
 |
|
|
 |
 |
|
|
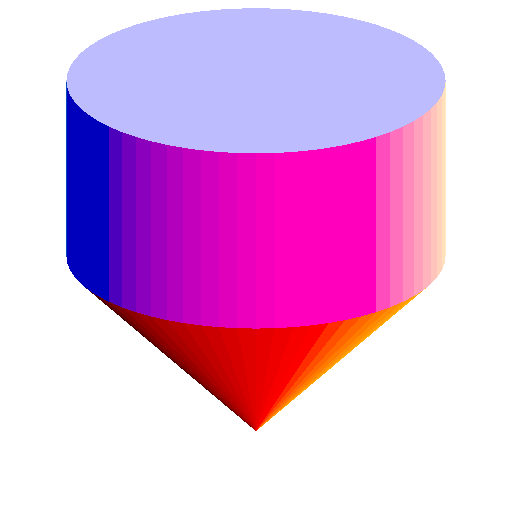 |
|
|
|
|
 |
| Image + Name | Description | Symmetry | Dual |
|---|---|---|---|
|
|
|
|
|
 |
|
|
 |
 |
|
|
 |
 |
|
|
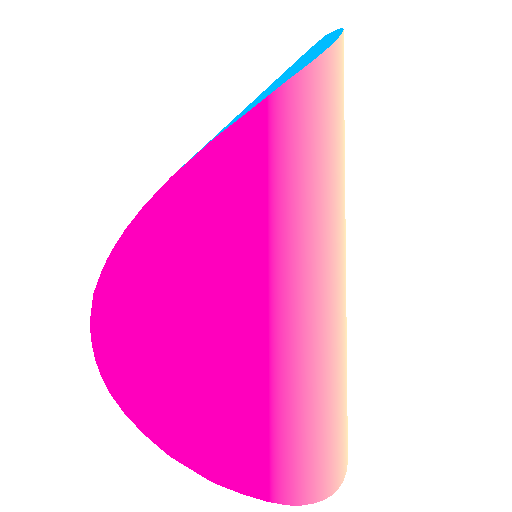 |
| Image + Name | Description | Symmetry | Dual |
|---|---|---|---|
 |
|
|
 |
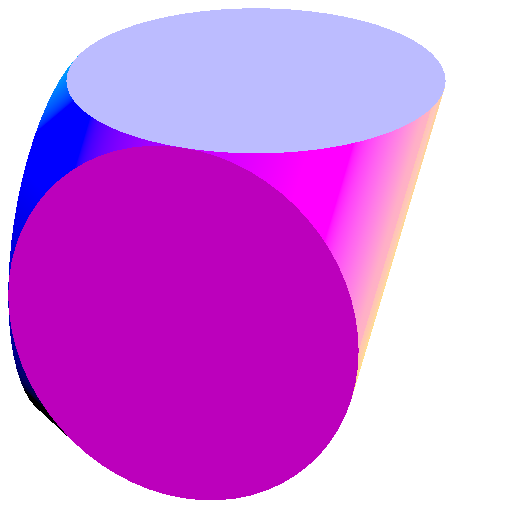 |
|
|
|
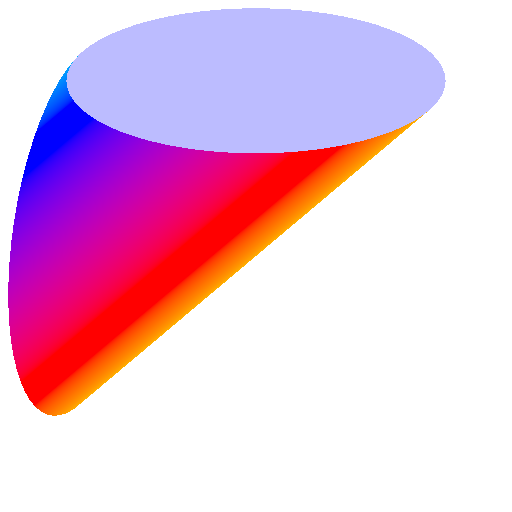 |
|
|
|
 |
|
|
|
 |
|
|
|
 |
|
|
|
the one and only
| Image + Name | Description | Symmetry | Dual |
|---|---|---|---|
 |
|
|
 |
 |
|
|
 |
 |
|
|
 |